
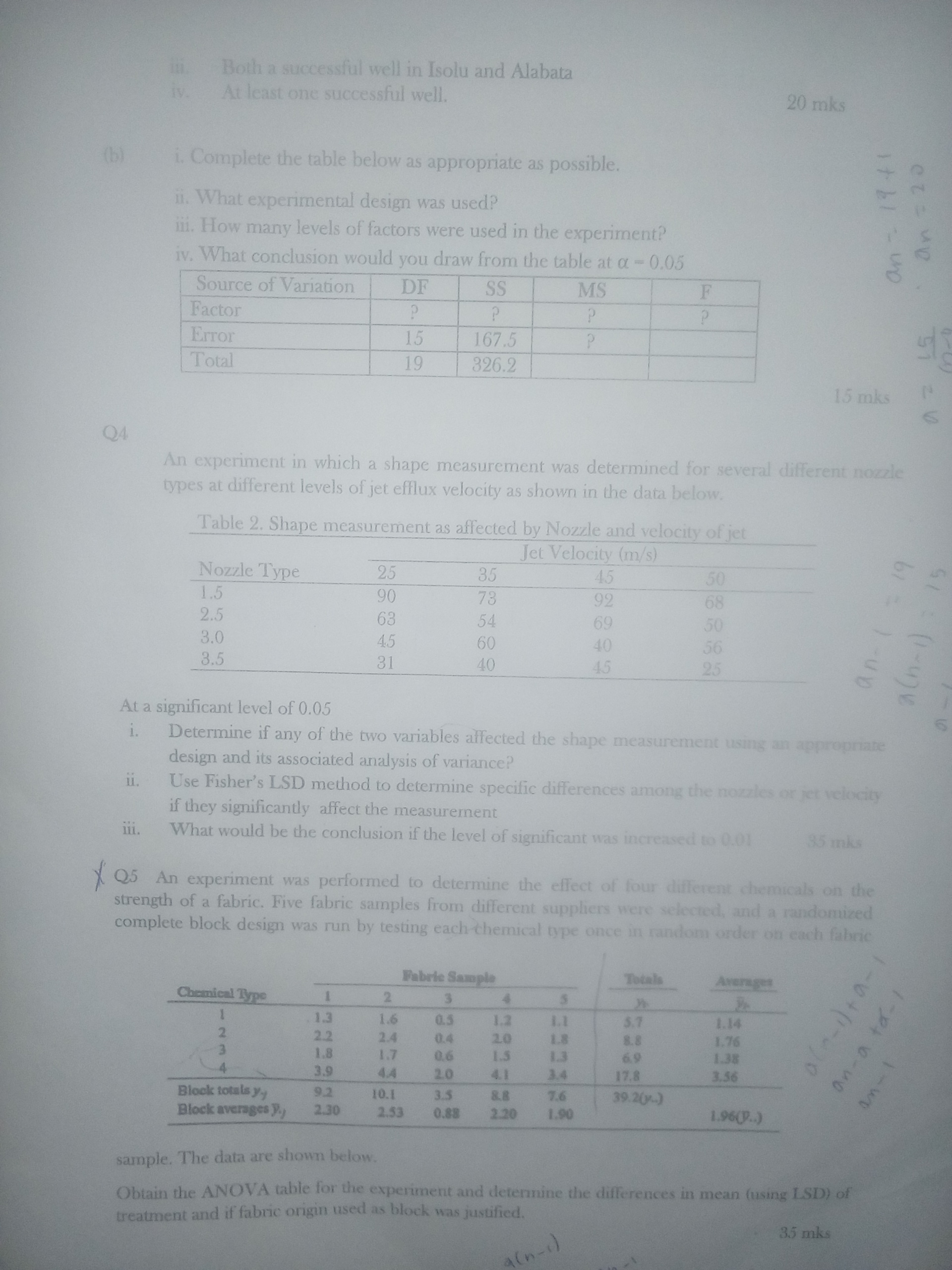
(i) Discuss statistical hypothesis
(ii) Discuss descriptive statistics and inductive statistics
(iii) What are qualitatively and quantitative variables?
(iv) Differentiate Sampling and sampling techniques
(v) Differentiate One tail test and two tails test and state hypotheses associated with them
(vi) What is the meaning of ANOVA and its usefulness?
Q2
A 400Level student of engineering conducted an experiment to investigate how leaking current in a SOS MOSFETS device is affected by channel length. Four channel lengths were selected from six different suppliers. If the supplier was considered a nuisance factor, the following data was obtained.
Table1. leakages of MOSFETS wrt channel Length in millivolt
| SUPPLIERS | ||||||
|---|---|---|---|---|---|---|
| CHANNEL LENGTH | FEM | TEMI | RYN | TOM | JAN | GWEN |
| 1.5 | 90 | 78 | 92 | 68 | 75 | 79 |
| 2.5 | 63 | 54 | 69 | 50 | 72 | 62 |
| 3.0 | 45 | 60 | 40 | 56 | 39 | 48 |
| 3.5 | 31 | 40 | 45 | 25 | 22 | 33 |
Determine the following
(i) The hypothesis that mean leakage voltage does not depend on the channel length using α=0.05
(ii) Is it justified to have assumed that source of channel as a nuisance factor?
(iii) If (i) above is not true separate the mean leakage current using LSD and specify the differences in the channel length
Q3
(a) Emma oils is bidding the rights to drill a well in Alabata and another in Isolu. The probability it will drill well in Alabata is 40%. if it does, the successful probability is 45%. The probability it will drill a well in Isolu is 30%. If it does the successful probability of the well is 55%.
Calculate the probability the Emma Oils has:
(i) A successful well in Alabata.
(ii) A successful well in Isolu.
(iii) Both a successful well in Isolu and Alabata
(iv) At least one successful well.
(b) (i) complete the table below as appropriate as possible
(ii) What experimental design was used ?
(iii) How many levels of factors were in the experiment ?
(iv) What conclusion would you draw from the table at α=0.05
| Source of Variation | DF | SS | MS | F |
| Factor | ? | ? | ? | ? |
| Error | 15 | 167.5 | ? | |
| Total | 19 | 326.2 |
Q4
An experiment in which a shape measurement was determined for several different nozzle types at different levels of jet efflux velocity as shown in the data below.
Table 2. Shape measurement as affected by nozzle and velocity of jet
| Jet Velocity (m/s) | |||||
|---|---|---|---|---|---|
| Nozzle type | 25 | 35 | 45 | 50 | |
| 1.5 | 90 | 73 | 92 | 68 | |
| 2.5 | 63 | 54 | 69 | 50 | |
| 3.0 | 45 | 60 | 40 | 56 | |
| 3.5 | 31 | 40 | 45 | 25 | |
At a significant level of 0.05
(i) Determine if any of the two variables affected the shape measurement using an appropriate design and its associated analysis of variance?
(ii) Use Fisher's LSD method to determine specific differences among the nozzles or jet velocity if they significantly affect the measurement
(iii) What would be the conclusion if the level of significance was increased to 0.01
Q.5
An experiment was performed to determine the effect of four different chemicals on the strength of a fabric. five fabric samples from different suppliers were selected and a randomized complete block design was run by testing each chemical type once in random order on each fabric sample. The data are shown below
| fabric sample | Totals | Average | |||||
|---|---|---|---|---|---|---|---|
| Chemical type | 1 | 2 | 3 | 4 | 5 | ||
| 1 | 1.3 | 1.6 | 0.5 | 1.2 | 1.1 | 5.7 | 1.14 |
| 2 | 2.2 | 2.4 | 0.4 | 2.0 | 1.8 | 8.8 | 1.76 |
| 3 | 1.8 | 1.7 | 0.6 | 1.5 | 1.3 | 6.9 | 1.38 |
| 4 | 3.9 | 4.4 | 2.0 | 4.1 | 3.4 | 17.8 | 3.56 |
| block total | 9.2 | 10.1 | 3.5 | 8.8 | 7.6 | 39.2 | |
| block average | 2.30 | 2.53 | 0.88 | 2.20 | 1.90 | 1.96 | |
...................
